기본도형의 작도

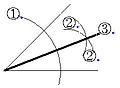
각의 이등분선

1. 점 O를 중심으로 하는 적당한 크기의 원을 그려 반직선 OX, 반직선 OY와의 교점을 각각 A, B라고 한다.

2. 점 A, B를 중심으로 하고 반지름 길이가 같은 두 원을 그려, 그 교점을 P라고 한다.

3. 반직선 OP를 그린다.

증명

선분 OA=선분 OB, 선분 AP=선분 BP, 선분 OP는 공통 (SSS합동) 각 AOP와 각 BOP가 서로 대응각이므로 선분 OP는 각의 이등분선이다.

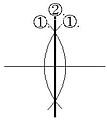
선분의 수직이등분선

4. 선분의 양 끝점을 중심으로, 반지름이 선분의 반보다 적당히 큰 원을 둘 그린다.

5. 두 원이 만나서 생기는 교점끼리 잇는다.

증명

위와 같이 하면 마름모가 그려진다. 마름모의 대각선의 성질은 서로 수직 이등분한다는것이다. 따라서, 위의 선분은 수직이등분된다.

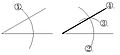
크기가 같은 각 

6. 점 O를 중심으로 하는 적당한 크기의 원을 그려 반직선 OX, 반직선 OY와의 교점을 각각 A, B라고 한다.

7. 컴퍼스 크기를 그대로 하여 점 P를 중심으로 하는 원을 그려 반직선 PQ와의 교점을 D라고 한다.

8. 점 D를 중심으로 하고 선분 AB를 반지름으로 하는 원을 그려 위 원과의 교점을 C라고 한다.

9. 반직선 PC를 그려 각 CPD를 만든다.

수선 (평각의 이등분)

10. 점 P를 중심으로 적당한 크기의 원을 그려서 직선 l과 만나는 교점을 각각 A, B라고 한다. (점P는 직선l위에 있지 않다.)

11. 점 A를 중심으로 적당한 원을 그린다.

12. 점 B를 중심으로 반지름 길이가 위와 같은 원을 그린다. 그리고 위 원과의 교점을 Q라고 한다.

13. 직선 PQ를 그린다.

선분의 등분

만약 어떤 선분을 a등분하고 싶다고 할때의 등분법은 다음과 같다.

14. 등분하고자 하는 선분에서 임의의 각도로 반직선을 하나 긋는다.

15. 반직선의 시작점에서 일정한 길이씩 떨어진a개의 점을 만든다.

16. 가장 끝의 점과 선분의 반직선과 접하지 않은 끝을 잇는다.

17. 3번의 선분과 평행하고 두 번째 점과 접하는 직선을 그린다.

점이 끝날때까지 평행한 선을 계속 그린다.

정삼각형

18. 선분의 양 끝 점에서 반지름이 선분과 같은 두 원을 그린다.

19. 이때 생기는 교점과 선분 양 끝점을 잇는다.

평행선 

20. 점 P를 지나면서 직선 l과 만나는 직선을 그어 그 교점을 점 A라고 한다.

21. 점 A를 중심으로 적당한 크기의 원을 그려 직선 PA, 직선 l과의 교점을 각각 B, C라고 한다.

22. 점 P를 중심으로 반지름의 길이가 위와 같은 원을 그려 직선 PA와의 교점을 점 Q라고 한다.

23. 점 B를 중심으로 반지름의 길이가 선분 BC와 같은 원을 그린다.

24. 점 Q를 중심으로 반지름의 길이가 4. 와 같은 원을 그려 3. 원과의 교점을 점 R이라고 한다.

25. 직선 PR을 그린다.

직각의 3등분 

임의의 각을 3등분 하는 작도는 3대 작도 불가능 문제 중 하나지만, 정삼각형을 이용하면 30도를 작도할 수 있으므로 직각은 3등분할 수 있다. 직각의 삼등분 순서는 다

음과 같다.

26. 직각에서 임의의 반지름을 가지는 호 AB를 그린다. (이하 호의 중심은 O)

27. A를 중심으로 1과 같은 반지름을 가지는 호 OD 를 그린다. (이때 D는 호 AB와 원 A 의 교점)

28. B를 중심으로 1과 같은 반지름을 가지는 호 OE 를 그린다. (이때 E는 호 AB와 원 B 의 교점)

29. O 와 D,E 를 이으면 직각이 삼등분된것이다.

 

각의 이등분선 선분의 수직이등분선 크기가 같은 각 수선(평각의 이등분선) 선분의 3등분 정삼각형

<출처:네이버오픈백과>